|
Symmetrie der Tasten
von
Herbert Henck
Einleitung
Die erste Form der Anordnung
Die zweite Form der Anordnung
Die dritte Form der Anordnung
Die doppelte Proportion 5 : 7 und Resümee
Zwei Nachträge (September 2016)
Anmerkungen
Einleitung
Weiß man um den Zusammenhang unserer Klaviatur mit den Kirchentonarten, deren Anfänge weit in die vorchristliche Antike zurückreichen, und weiß auch um
die neuzeitliche Ergänzung fehlender Halbtonschritte durch Obertasten in der ursprünglichen Untertastenreihe mit dem Ziel einer vollständigen Chromatik, so verwundert doch, dass sich trotz der komplexen und
langen Entstehungsgeschichte der Klaviatur zwei Symmetrien in ihr finden lassen. [1] Diese beiden Symmetrien – die eine mit der Untertaste d, die andere mit der Obertaste gis als Spiegelachse – sind zwar nur in seltensten Ausnahmefällen musikalisch zum Tragen gekommen, doch scheint mir die Frage von Interesse, ob es sich bei diesen Symmetrien um einen glücklichen Zufall, um Theorie und Absicht der Klavierbauer oder um eine mathematische Notwendigkeit handelt, die gar keine Alternative erlaubt.
Untersucht wird daher unter anderem die Frage, ob eine veränderte Stellung (Permutation) der zwei Halbtonschritte in der Untertastenreihe zu vergleichbaren
oder ähnlichen Symmetrien wie denen der heutigen Klaviatur führt. Alle anderen Merkmale der Klaviatur werden dagegen übernommen, also die 12 Töne und Tasten bis zur ersten Tonwiederholung, die Aufteilung in 7 Unter-
und 5 Obertasten oder die Eigenheit, dass zwei nebeneinanderliegende Untertasten einmal einen Halbtonschritt, ein andermal einen Ganztonschritt bedeuten können, eine Eigenheit, die sich als Skordatur bezeichnen
ließe, ebenfalls auf die Modi der Kirchentonarten zurückgeht und sich in übertragener Form in unserer traditionellen Notation wiederholt. [2] Dass die
im Rahmen dieser Untersuchung zutage tretenden Tastensysteme nur noch sehr bedingt mit den historischen Kirchentonarten in Verbindung stehen, ist begreiflich. Ansonsten sei noch einmal gesagt, dass unter der
behandelten Symmetrie jene Spiegelung der Tastenanlage um eine Achse verstanden wird, die entsteht, sobald ein mit der Achse beginnendes simultanes chromatisches Aufwärts- und Abwärtssteigen stets auf dieselbe Tastengattung trifft, also auf zwei Unter- oder zwei Obertasten.
Sieht man, dass die 5 Obertasten der Klaviatur in ihrer heutigen Form sich in zwei Gruppen zu 2 + 3 Tasten gliedern, so gilt diese Addition natürlich auch
in umgekehrter Richtung, da die Folge der Obertasten davon abhängt, wo man beginnt und welche Richtung man einschlägt. Anstelle von 2 + 3 könnte es ebenso heißen 3 + 2 oder angesichts der
beiderseitigen Erweiterung der Oktave … 3 + 2 + 3 + 2 + 3 + 2 …, wodurch sich das vertraute Klaviaturmuster ergibt. In dieser Zahlenstruktur scheinen die Symmetrien auch ohne die Untertasten schon durch,
da man eine beliebige Zahl auswählen kann und dann gleichzeitig nach links und rechts fortschreitend immer auf identische Größen trifft. Liegt die eine dieser beiden Symmetrien in der Mitte der „2“
zwischen den beiden Obertasten auf der Untertaste d, so ist die andere Spiegelachse die mittlere Taste in der „3“ als Obertaste gis.
In nachstehenden Abbildungen sind die Töne der chromatischen Skala nur anfangs benannt und später dann von 1 bis 12 nummeriert, da es für die behandelten
Fragen letztlich ohne Belang ist, mit welchem Ton oder welcher Taste man beginnt. Entscheidend ist, dass die Chromatik der Töne sich in den Tasten systematisch abbildet und akustische und mechanische, ton- und
tastenweise Fortschreitung einander entsprechen.
Auch wenn die Stellung der Obertasten von den Untertasten und den dort vorliegenden Intervallen bestimmt wird, so entwickeln die Obertasten durch ihre Form
und Farbe doch eine Autonomie, die sie dem bloßen Reflex entziehen, wie eine eigenständige Anlage mit eigenen Gesetzen wirken und ihrerseits Rückschlüsse auf die Untertasten zulassen. Dabei tritt die Gliederung
der Obertasten in 2 + 3 so deutlich hervor, dass leicht übersehen werden kann, sie sei nur eine von den Untertasten bedingte, denn die Reihe der Untertasten wirkt durch ihre Geschlossenheit und
Einheitlichkeit gleichsam als neutrale und selbstverständliche Ebene. Damit die Gruppen von Obertasten aber überhaupt als Gruppen sichtbar werden können und ihre Gestalten sich klar voneinander abheben
– was für die Spieler eine durchaus wichtige Eigenschaft ist –, werden zwei Regeln erkennbar (da die verschiedenen Intervalle der Untertastenreihe nicht sichtbar, sondern nur hörbar sind,
bietet es sich an, in diesem Fall von den gliedernden und gegliederten Obertasten auszugehen):
1.) Nach jeder Obertaste folgt eine Untertaste; oder anders gesagt: Nie stehen zwei Obertasten unmittelbar nebeneinander, sondern sie sind immer getrennt. Dies bedeutet akustisch, dass es keine kleinen Sekunden oder große Septimen und in der heutigen Klaviaturform auch keine Tritoni zwischen zwei Obertasten gibt. Die Erklärung ist in der komplementären, lückenfüllenden Funktion der Obertasten und ihrem Bezug auf die Intervalle der Untertastenreihe zu suchen.
2.) Ebenso stehen vor und nach jeder Obertastengruppe jeweils mindestens zwei Untertasten, so dass die Abstände zwischen den Gruppen auch mindestens
doppelt so groß sind wie innerhalb der Gruppen. Die von den Untertasten bewirkten Abstände gliedern die Obertasten in Gruppen, die erst hierdurch der optischen und haptischen Wahrnehmung als Einheiten gut zugänglich
werden und sich von den Instrumentalisten schnell und sicher auffinden lassen.
Diese zwei Bedingungen bewirken, dass sich bei sieben zur Verfügung stehenden Untertasten pro Oktave lediglich drei Gruppierungen von je fünf
Obertasten bilden lassen (7 Untertasten + 5 Obertasten = 12 Tasten oder Töne pro Oktave), nämlich:
Stellt man die Möglichkeiten der Fünferbildung systematisch zusammen, erhält man
Die zweite Hälfte entsteht aus der rückwärts gelesenen ersten Hälfte und kann daher, wie oben gezeigt, entfallen, so dass insgesamt nur 3 Möglichkeiten
übrigbleiben, von denen die unter a) genannte unserer bekannten Klaviatur entspricht.
Mathematisch scheinen sich noch weitere Gliederungen der 5 Obertasten anzubieten (etwa 1 + 1 + 3 oder 2 + 2 + 1), doch sobald man mehr als
2 Obertastengruppen in einer Oktave bildet, reicht die Menge von 7 Untertasten nicht mehr aus, jeder Obertastengruppe beidseitig mindestens 2 Untertasten folgen zu lassen: Bei 1+1+3 oder bei 2+2+1 Obertasten würde man beidemale mindestens 8 Untertasten benötigen. Die Anzahl der Untertasten, die für die Gliederung zur Verfügung steht, beschränkt somit zugleich die Anzahl der Obertastengruppen.
Die erste Form der Anordnung
Die erste Abbildung zeigt die Gestalt der uns vertrauten Klaviatur:

Abb. 1
Zum Verständnis dieser und der folgenden Abbildungen sei bemerkt, dass die Formen
und Abstände der Tasten stilisiert sind und somit die Verfahren der Klavierbauer vernachlässigen, durch Winkelschnitte oder feinste Breitenunterschiede der Tasten die Bespielbarkeit der Klaviatur
zu verbessern. Symmetrieachsen sind mit x (weiße Untertasten) oder y (schwarze Obertasten) unterhalb der Tasten gekennzeichnet.
Auf die beiden anderen Möglichkeiten sei nachfolgend noch näher eingegangen.
Gemeinsam ist ihnen, dass sie nicht mehr auf einem geschichtlich überlieferten Modus gründen, sondern von den Obertasten ausgehen, die nun umgekehrt zwei Modi
erzeugen. Würde man diese zwei neuen siebentönigen Modi wie üblich auf die mit c = 1 beginnende Untertastenreihe legen, ergäben sich folgende Skalen (Abb. 2 und Abb
. 3):
c cis d dis e f fis g gis a ais h (Obertasten beidemal
hochgestellt)
und
c cis d dis e f fis g gis a ais h
Die zweite Form der Anordnung
Eine zweite Möglichkeit besteht darin, die fünf Obertasten jeweils in Gruppen
von 1 + 4 aufzuteilen, wobei wiederum auch das Umgekehrte, nämlich 4 + 1 richtig wäre. Ins Innere der Vierergruppe kämen 3 Untertasten (5, 6, 7), vor und hinter
dieselbe Gruppe jeweils 2 Untertasten (3-4 bzw. 1-2) zu stehen, die zugleich den Abstand zu der vorausgehenden oder folgenden „Einergruppe“ festlegen:
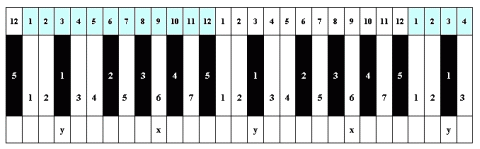
Abb. 2
Schnell erkennt man in der Abbildung, dass auch bei dieser Anordnung zwei Symmetrien zustande kommen, deren Achsen erneut mit x und y bezeichnet sind. Wie
in der traditionellen Klaviaturform ist die Achse einmal eine Ober-, einmal eine Untertaste, und dort wie hier liegen die beiden Achsen im Intervall eines Tritonus auseinander, der die Oktave halbiert.
Die dritte Form der Anordnung

Abb. 3
Auch die dritte Möglichkeit, die Obertasten zu gruppieren, führt, wie Abb. 3 zeigt, zu
den bereits beschriebenen zwei Symmetrien (siehe x und y), sowohl im Hinblick auf die Tastengattungen als auch auf das Tritonus-Intervall. Man sollte die zwei
Untertastenpaare, die in Abb. 1 und 2 zu sehen sind, hier nicht vermissen, denn liegen die drei Untertasten unmittelbar nebeneinander, so ist die Bedingung erfüllt, dass
mindestens 2 Untertasten die Obertastengruppe beidseitig einrahmen müssen, während im Innern der Obertastengruppen jede Obertaste von der nächsten durch nur 1 Untertaste getrennt ist.
Aufgrund dieser Übereinstimmungen und erkennbaren Gesetzmäßigkeit lässt sich
zumindest sagen, dass die Symmetrien im Aufbau unserer Klaviatur nicht irgendwie Absicht ihrer Erbauer gewesen sein können und ihnen primär keine musikalische
Aufgabe zukam, sondern dass sie durch die spezifischen Vorgaben der Tastenmengen bewirkt wurden. Der Ausbau der Kirchentonarten zur Chromatik stand aber völlig
im Vordergrund, und somit sind die Symmetrien nur ein Automatismus, der auch unabhängig von Tasten und Tönen existiert und die Möglichkeiten der Anordnung von
Elementen begrenzt. Dies erklärt vielleicht, warum der musikalische Gebrauch dieser Symmetrien, soweit mir bekannt ist, auch erst in der Moderne stattfand. [3]
Dass den vorstehenden Untersuchungen fünf Obertasten zugrunde gelegt wurden,
war bereits eine Folge des Umstandes, dass in der Untertastenreihe an fünf Stellen Ganztonschritte vorlagen, die sich durch fünf Obertasten oder Halbtonschritte
zu 7 + 5 = 12 chromatischen Tönen pro Oktave ausfüllen ließen. Unter der Voraussetzung, dass nicht mehr als sieben Untertasten zur Verfügung stehen, und unter
Beachtung der Regeln, die sich von der traditionellen Klaviatur abnehmen lassen, stellten sich die Symmetrien stets zwangsläufig ein und erwiesen sich als unabhängig
von der Gruppierung der fünf Obertasten. Diese Gruppierungen konnten schließlich nur auf drei Arten stattfinden, nämlich als 2 + 3, als 1 + 4 oder als 5 + 0, wobei die
Umkehrung der Summanden ohne Bedeutung ist.
Nähme man an, dass in der Untertastenreihe nur ein einziger Ganztonschritt vorläge,
käme es nur zu einer einzigen ergänzenden Obertaste pro Oktave; andererseits müssten dann alle übrigen Halbtonschritte auf den Untertasten vorhanden sein, was deren Zahl
auf 11 Töne (Tasten) pro Oktave erhöhen würde (10 Halbtonschritte + 1 Ganztonschritt). Diese Form der Anordnung würde allerdings infolge der 11
nebeneinanderliegenden Untertasten zu Spannungen aller Art in den Händen führen und dem Bedürfnis zuwiderlaufen, etwa Oktaven mit einer Hand allein bequem greifen zu
können. – Eine numerische Ausgeglichenheit zwischen Unter- und Obertasten (je sechs Ganztonschritte) würde dagegen die Oktave enger werden lassen, als sie heute ist. Der
große Nachteil dieser Form wäre jedoch, neben zu kleinen Abständen für die Hände, eine sehr große Unübersichtlichkeit des Tastenbildes, da so nur ein gleichförmiges
Muster entstünde, in welchem sich ein bestimmter Ton nicht mehr mit derselben Sicherheit anschlagen ließe und welches dazu führen würde, ein jedes c beispielsweise rot einzufärben.
Die doppelte Proportion 5 : 7 und Resümee
Angeregt durch vorstehende Beobachtungen suchte ich nach weiteren numerischen
Zusammenhängen zwischen Unter- und Obertasten. Hierbei fiel mir insbesondere die Proportion 5 : 7 auf, da man ihr in der herkömmlichen Klaviatur in doppelter Form
begegnet. Denn zum einen bezeichnet jenes Verhältnis das der Tastengattungen (also das der Obertasten zu den Untertasten); zum anderen ist 5 : 7 auch die Proportion von
zwei aufeinanderfolgenden, sich zur Zwölfzahl ergänzenden tastensymmetrischen Abschnitten der chromatischen Skala. Sind im ersten Fall die Tasten ihrer traditionellen
Anlage entledigt und rein mengenmäßig verglichen, so durchdringen sie sich im andern Fall hoquetusartig unter Beibehaltung ihrer zwei spezifischen spiegelsymmetrischen
Anordnungen und Aufteilungen in Unter- und Obertasten, die theoretisch nach oben und unten ins Unendliche fortschreiten und praktisch nur vom individuellen Hören
begrenzt werden. Die folgende Abbildung macht den doppelten Bezug durch die Zahlen über und auf den Tasten kenntlich.
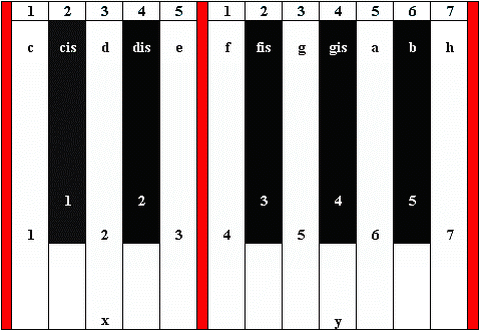 |
Abb. 4
Der erste Fall, in dem die Mengen der Ober- und Untertasten pro Oktave verglichen
werden, ist hinlänglich bekannt und bedarf keiner zusätzlichen Erklärung; die Proportionen lassen sich in Abb. 4 von den auf die Tastenoberflächen geschriebenen
Zahlen und den Tonnamen ablesen. Der zweite Fall wird spätestens deutlich, sobald man sich eine Trennlinie (rot in vorstehender Abb. 4 [4]) zwischen allen weißen, nur
einen Halbtonschritt ausmachenden Tastenpaaren vorstellt, also jeweils zwischen e und f bzw. h und c. Diese Unterteilung hebt nicht nur die beiden Symmetrien in der
Tastenanlage (mit d als x-Achse, gis als y-Achse) hervor, sondern man erkennt auch, dass diese zwei Tastengruppen die autonomen, sich nirgends überlagernden Kerne der
Symmetrien bilden, die ebenfalls im Verhältnis von 5 : 7 zueinander stehen. Durch die Zahlen in der obersten Zeile von Abb. 4 ist dies verdeutlicht: Der erste Abschnitt hat
die fünf Töne c-cis-d-dis-e, der zweite die sieben Töne f-fis-g-gis-a-b-h. Die beiden Obertastengruppen sind dabei auf dieselbe Art in und zwischen Untertasten eingebettet:
Nach links und rechts schließen an jede Obertastengruppe zwei Untertasten an, während im Gruppeninnern je eine Untertaste zwischen zwei aufeinanderfolgenden
Obertasten steht. Für beide Abschnitte ließe sich daher als Regel ableiten:
T = O + (O + 1)
oder verkürzt:
T = 2 O + 1
T = Tastensumme des symmetrischen Abschnitts; O = Obertasten-Anzahl
Die Rechnung macht auch hier jedoch nur Sinn, solange 12 als Tastensumme aus
7 Unter- und 5 Obertasten, also die große Septime, nach welcher die oktavierende Verdopplung von Tonhöhen erfolgt, nicht überschritten wird.
In Abb. 2 hätte man 2 Obertastengruppen, bestehend aus 1 + 4 Obertasten, so dass man einerseits 1 Obertaste + 2 Untertasten = 3 sowie andererseits 4 Ober- + 5 Untertasten = 9 als Anzahl der Tasten pro Gruppe erhielte, was
zusammengenommen die 12 Tasten bzw. Töne ergibt: 3 + 9 = 12.
Und in Abb. 3 hätte man entsprechend 5 Ober- + 6 Untertasten = 11 Tasten sowie bei
einer einzigen Untertaste 0 + 1 = 1, so dass man auch hier als Summe 11 + 1 = 12 Tasten = Töne erhält. Bei einer Gruppe aus nur 1 Untertaste kann man natürlich
keine rote Trennlinie einzeichnen, doch wäre diese Untertaste insgesamt rot zu färben, da nun sie die zwei benachbarten Elfergruppen links und rechts als Symmetrieachse trennt.
Die drei Möglichkeiten seien nochmals zusammengestellt:
1.) 5 + 7 = 12 Tasten: Abb. 4 mit den roten Linien; traditionelle Klaviatur
2.) 9 + 3 = 12 Tasten: Abb. 2 Auch hier denke man sich rote Linien
zwischen den Untertasten 1-2 und 3-4.
3.) 11 + 1 = 12 Tasten: Abb. 3 Hier wäre die Untertaste 7 selbst die Achse x
der Symmtrie, die nur aus 1 Taste = Ton
bestünde und daher auch rot zu färben wäre
Auch diese drei Additionen weisen auf eine mathematische Notwendigkeit hin, da ohne
Wiederholung sämtliche Paare aus ungeraden Zahlen benutzt werden, die zwischen 1 und 12 liegen und als Summe 12 bilden. Dass diese Paare stets nur aus den ungeraden
Summanden 1, 3, 5, 7, 9 und 11 bestehen, ist zum einen auf die Symmetrie der Tasten zurückzuführen, die jeweils mit einer einzigen Taste als Achse der Symmetrie beginnt (d oder gis) und sich dann nach oben und unten gleichzeitig durch Hinzufügen eines
Tastenpaares der komplementären Gattung erweitert (1 + 2 + 2 + 2 + 2 + 2 + 1).
Zum andern können nur zwei gerade oder zwei ungerade Summanden die erforderliche Zwölfzahl bilden, nicht aber ein gerader und gleichzeitig ein ungerader Summand, denn
auf folgende Weise werden alle ganzzahligen Werte erfasst: 1 + 11 = 2 + 10 = 3 + 9 = 4 + 8 = 5 + 7 = 6 + 6 = 12 und umgekehrt, da die Abfolge der Summanden ja keinen
Einfluss auf das Ergebnis der Additionen hat.
Für die uns vertraute Form der Klaviatur wird nunmehr deutlich, dass sie
in wesentlichen Punkten von den siebentönigen Modi der Kirchentonarten abhängig ist. Ungeachtet der Tatsache, dass der Aufbau dieser Modi sowohl aus kleinen wie großen
Sekunden besteht, wurden sie zum praktischen Gebrauch unterschiedslos auf eine Reihe gleichartiger Tasten (die späteren Untertasten) übertragen, und
erst nach Einführung von Obertasten konnten sie zu einer nur scheinbar neutralen Untertastenreihe werden, denn die optische Gliederung der Tastatur verdankt sich
heute wohl mehr den Ober- als den Untertasten. Die Ordnung dieser Grundlage entschied gleichwohl über das Weitere: über die Stellung der Obertasten ebenso wie
über die Einteilung der Tastatur in Abschnitte, über die Proportionen von Unter- und Obertasten oder die sich erst jetzt zur Zwölfzahl ergänzenden Symmetrien. Diese
Symmetrien sind, solange Obertasten noch fehlten, nicht sichtbar, sondern nur hörbar, denn sie spielten sich ausschließlich im Bereich der akustischen Intervalle, nicht der
Tastengattungen ab, und sie haben durch die doppelte Belegung kein optisches oder haptisches Äquivalent (von d ausgehend erhält man: d–c/e–h/f–a/g–g/a–f/h–e/c–d/d
usw.; die andere, infolge des fehlenden Ausgangstons stärker beschränkte, ist: g/a–f/h–e/c–d/d–c/e–h/f–a/g usw.). Hierbei sieht man, dass die zweite
Symmetrie in der ersten bereits enthalten ist, sofern man allein die Tonhöhen betrachtet und die Oktavversetzungen außer Acht lässt. Es ließe sich daher behaupten, dass alle
hier untersuchten Eigenschaften der heutigen Klaviatur auf die in der Untertastenreihe angelegten Modi der Kirchentonarten zurückzuführen sind und erst durch die
Einführung von Obertasten weiterhin entfaltet wurden.
*
Schließlich sei noch eine Übereinstimmung der Tastenanlage mit der Gestalt der Hand erwähnt, welche, zur Faust geschlossen, von dem Auf und Ab der nun hervortretenden
Fingerknöchel und den sich anschließenden Vertiefungen ausgeht. Diese bekanntlich als Eselsbrücke verwendete Ordnung klärt so sinnfällig wie schnell, welche Monate im
heute gebräuchlichen Gregorianischen Kalender 31 und welche 30 oder weniger Tage haben. Anstelle der Knöchel, die natürlich schneller als jede Klaviatur zur Hand sind,
könnte man mit demselben Ergebnis die gewöhnliche Tastenanlage benutzen, wenn in aufsteigender Weise die längeren Untertasten für die längeren Monate, die kürzeren
Obertasten für die kürzeren Monate stehen. Man muss hier allerdings mit dem Ton f beginnen, will man die Töne in Übereinstimmung mit den Monaten bringen.
1.) Januar = f, 2.) Februar = fis, 3.) März = g, 4.) April =
gis, 5.) Mai = a,
6.) Juni = ais, 7.) Juli = h
, 8.) August = c, 9.) September = cis, 10.) Oktober = d, 11.) November =
dis, 12.) Dezember = e
[13.) = 1.)]
Rot sind Obertasten: Monate mit 31 Tagen
Blau sind Untertasten: Monate mit 30 Tagen und weniger
Da beide Muster, also das der Klaviatur und wie das des Gregorianischen Kalenders, auf die Zeit der Renaissance zurückzugehen scheinen, liegt hier möglicherweise, mehr
vermag ich nicht zu sagen, ein Zusammenhang vor.
*
Zwei Nachträge (September 2016)
Die Proportion 5 : 7 ist auch in der experimentellen Tastatur von Karl Bernhard
Schumann vorhanden (1859). Zwar nicht als Ober- oder Untertasten, aber als Färbung der Tasten, die unabhängig ist von der Tastengattung: 2 + 4 Obertasten
sowie 3 + 3 Untertasten = 12 Tasten oder Tonhöhen; 7 weiße + 5 schwarze Tasten = 12 Tasten oder Tonhöhen. Insgesamt werden hier pro Oktave 6 Ober- und
6 Untertasten gegenübergestellt, während die Einfärbungen 5 schwarze und 7 weiße Tasten zeigen. Eine Abbildung dieser Klaviatur ist in dem zweiteiligen Aufsatz Klaviaturen, Teil 1, Kapitel 4 hier zu sehen: Die Belegung der Tasten 1–5 ist die
traditionelle, die der folgenden Tasten 6–12 kehren die heutige Schwarz- und Weißfärbung aber modifiziert um, wobei die auf Untertasten befindlichen
Halbtonschritte auf weiße Obertasten umverteilt sind. So kommt es, dass die C-Dur-Tonleiter weiterhin zunächst auf ausschließlich weißen Untertasten gespielt wird, doch
setzt sich mit dem vierten Ton diese Tonleiter auf nunmehr weißen Obertasten fort.
Beim zurück- oder umkehrenden Zählen der Fingerknöchel einer geschlossenen Hand erhält man 1 2 3 4 5 6 7 Zahlen bzw. bei entsprechendem Zählen der Vertiefungen zwischen den Fingern: 1 2 3 4 5 Zahlen, was ebenfalls als Proportion 7 : 5 ergibt. Genauer ausgedrückt liegen die Wendepunkte der beiden gut überschaubaren Folgen ABCDCBA und XYZYX jeweils in der Mitte, wobei auch ein versaler Buchstabe nur
ein einziges Mal, alle anderen aber doppelt in beiden Folgen erscheinen: 4 Knöchel aufwärts + 3 abwärts = 7 Knöchel; bzw. 3 Vertiefungen aufwärts + 2 abwärts = 5 Vertiefungen. Somit bieten auch die Hände Anschauungsmaterial für die Proportion
7 : 5. Es ist dabei gleichgültig, welche Hand man nimmt. Mit diesen Überlegungen lässt sich jedoch die Zwölfzahl, die sich aus der Summe von 7 + 5 = 12 ergibt, aus der
vorgegebenen Gestalt der Hand ableiten, selbst wenn diese nachträgliche Bestätigung keine geschichtliche Rolle bei der Entwicklung der Zwölftontechnik spielte und das Verfahren etwas primitiv erscheinen mag.
*
Eine persönliche und gewiss nicht zu überschätzende Bemerkung sei hier ans Ende
gestellt, denn ich weiß aus den vorstehend ausgebreiteten Beobachtungen und Berechnungen keinerlei Schlüsse zu ziehen, und so muss ich es einstweilen bei der
Beobachtung als solcher bewenden lassen. Dass sich diese Art von Beobachtung indes nur mittelbar auf die Musik bezieht, die auf Klaviaturen zur Ausführung kommt, ist mir
gleichwohl hinreichend bewusst. Die hier behandelte Symmetrie ist vornehmlich eine sichtbare der Tasten, nicht eine hörbare der Töne, und transponiert man eine
Tastensymmetrie, wird schnell deutlich, dass die Wahrung der Intervallstruktur oft sehr rasch zu Unterschieden in den Tastengattungen führt. Eine Übertragung der Symmetrien
auf andere Instrumente würde die Tastensymmetrie sogar nahezu hinfällig machen. Auch vermag ich nicht zu sagen, ob das zweimalige Auftreten der Proportion 5 : 7 sich
lediglich einem Zufall verdankt oder auch eine Absicht einstiger Konstrukteure war. Beides schiene mir aber so erstaunlich wie bewundernswert. Zwar vermute ich, dass
die Vorgaben der Diatonik eindeutig waren und die Obertastenreihe und ihre Gliederung eine mathematisch notwendige Konsequenz waren, doch wären die
Ursachen für diese Notwendigkeit beidemale wohl in der Diatonik selbst zu suchen.
Anmerkungen
[1] Vergleiche hierzu den zweiteiligen Aufsatz Klaviaturen. Gestalt und
Bespielbarkeit, wo besonders der erste Abschnitt, Die Klaviatur als chiffrierte Chromatik, diese Symmetrien behandelt. Hier wird auch auf ihre musikalische
Umsetzung durch die Komponisten Bernhard Ziehn (1845–1912) und Kyle Gann (*1955) sowie die mehr pädagogische Nutzung durch den Pianisten und Musikologen Helmut Karl Heinz Lange (*1928) hingewiesen.
[2] Wie Anm. 1; hier der Abschnitt Klaviatur und Notation. Zusammenhänge von
Bespielbarkeit und Lesbarkeit.
[3] Wie Anm. 1.
[4] Dies sind in einer heutigen Klaviatur (nicht jener in obigen Abbildungen) die einzigen
beiden geraden, unverwinkelten Linien zwischen zwei Tasten (e-f und h-c), jeweils e und h an der rechten Tastenkante, f und c an der linken.
Entstanden in Deinstedt im Mai 2008 ( verschiedene Nachträge)
Erste Eingabe ins Internet: Dienstag, den 27. Mai 2008
Letzte Ãnderung: Dienstag, 27. September 2016
© 2008–2016 by Herbert Henck
|

